在物理学和工程学中,波动方程是一个至关重要的概念,它描述了波动现象的数学规律。波动方程有多种表达式,每种表达式都适用于不同的物理背景和情境。本文将详细探讨波动方程的三种主要表达式,包括一维波动方程、三维波动方程以及亥姆霍兹方程。这些表达式不仅在数学上具有深刻的意义,而且在物理学和工程学的实际应用中也发挥着重要作用。

首先,我们来看一维波动方程。在一维空间中,波动方程通常被表达为:

∂²u/∂t² = c²(∂²u/∂x²),
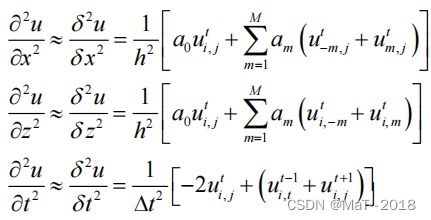
其中,u(x,t)代表在位置x和时间t处的波动位移或振幅;c是波速,它描述了波动在介质中传播的速度;∂/∂t和∂/∂x分别表示对时间和空间的偏导数。这个方程描述了波动如何随时间和空间变化。在一维情况下,波动可以看作是在一条直线上传播的,因此这个方程具有相对简单的形式。然而,它仍然能够捕捉到波动的一些基本特性,如反射、折射和干涉等。

接下来,我们考虑三维波动方程。在三维空间中,波动方程的形式变得更加复杂,但仍然保持了其基本结构。三维波动方程通常被表达为:
(1/c²)∂²u/∂t² = ∇²u,
其中,∇²是拉普拉斯算子,它在三维空间中定义为:
∇² = ∂²/∂x² + ∂²/∂y² + ∂²/∂z²,
这个方程描述了波动在三维空间中的传播情况。与一维波动方程相比,三维波动方程考虑了更多的空间维度,因此能够更准确地描述波动在复杂介质中的传播行为。例如,在地震学中,三维波动方程被用来模拟地震波在地球内部的传播情况;在声学工程中,它被用来预测声波在房间或建筑物内的传播路径和强度分布。
除了上述两种基本的波动方程外,还有一种重要的表达式被称为亥姆霍兹方程。亥姆霍兹方程是波动方程在特定条件下的简化形式,通常用于描述在静态或稳态条件下的波动行为。在三维空间中,亥姆霍兹方程可以表达为:
∇²u + k²u = 0,
其中,k是波数,它定义为ω/c,其中ω是波动的角频率。这个方程在描述电磁波、声波和其他类型的波动时具有广泛的应用。例如,在电磁学中,亥姆霍兹方程被用来描述电磁波在均匀介质中的传播情况;在光学中,它被用来研究光的衍射和干涉现象;在量子力学中,它还与薛定谔方程有密切的联系,用于描述微观粒子的波动行为。
值得注意的是,波动方程的这三种表达式并不是孤立的,它们之间存在着紧密的联系和相互转化关系。例如,在一维情况下,通过傅里叶变换可以将时间域中的波动方程转换为频率域中的亥姆霍兹方程;在三维情况下,通过分离变量法或其他数学技巧也可以将波动方程化简为亥姆霍兹方程的形式。这种相互转化关系不仅为波动方程的研究提供了更多的数学工具和方法,也为波动现象的实验观测和理论分析提供了更广泛的视角和思路。
此外,波动方程的解也是波动现象研究中的重要内容。根据波动方程的具体形式和初始条件、边界条件等约束条件的不同,波动方程的解可能具有不同的形式。例如,在一维情况下,波动方程的解可能是正弦波、余弦波或它们的叠加形式;在三维情况下,解可能更加复杂,包括球面波、平面波和复杂的波前形状等。这些解不仅描述了波动的传播特性,还揭示了波动与介质之间的相互作用规律。
在实际应用中,波动方程的解对于理解和预测波动现象具有重要意义。例如,在地震学中,通过求解三维波动方程可以预测地震波的传播路径和强度分布,为地震预警和抗震设计提供重要依据;在声学工程中,通过求解波动方程可以优化声学系统的性能,提高声音的质量和清晰度;在电磁学中,通过求解波动方程可以设计更高效的电磁波传输和接收设备,推动无线通信和雷达技术的发展。
总之,波动方程的三种表达式——一维波动方程、三维波动方程和亥姆霍兹方程——在物理学和工程学中发挥着重要作用。它们不仅描述了波动现象的基本规律,还为波动现象的实验观测和理论分析提供了强大的数学工具和方法。随着科学技术的不断发展,波动方程的研究和应用将会更加深入和广泛,为人类探索自然界的奥秘和推动科技进步做出更大的贡献。
































相关文章