二进制与十进制如何相互转换？

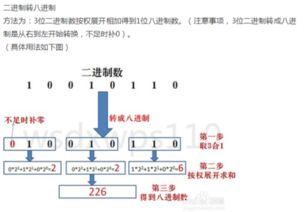
一、二进制如何转十进制

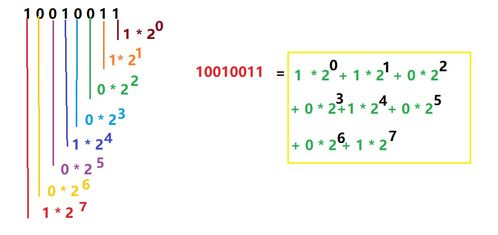
二进制转十进制的过程其实是一个权值累加的过程。在二进制数中，每一位上的数字都代表一个特定的权值，这个权值是2的幂次方，幂次方的指数从右到左递增，最右边的数字代表2的0次方，也就是1，向左每移动一位，幂次方的指数增加1。

二进制与十进制如何相互转换？ 3

举个例子，二进制数“1011”转换成十进制数的步骤如下：

二进制与十进制如何相互转换？ 4

1. 从右到左，确定每一位的权值。对于“1011”，最右边的“1”的权值是2^0=1，向左一位的“1”的权值是2^1=2，再向左一位的“0”的权值是2^2=4（虽然这一位是0，但权值仍需计算），最左边的“1”的权值是2^3=8。

2. 将每一位上的数字乘以它对应的权值，并将结果累加。即：1×2^0 + 0×2^1 + 1×2^2 + 1×2^3 = 1×1 + 0×2 + 1×4 + 1×8 = 1 + 0 + 4 + 8 = 13。

所以，二进制数“1011”转换成十进制数是13。

二、十进制如何转二进制

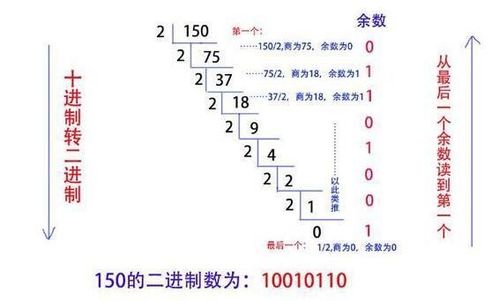
十进制转二进制的过程则是一个不断除2取余的过程。具体步骤如下：

1. 将十进制数除以2，得到商和余数。

2. 将商再次除以2，又得到一个新的商和余数。

3. 重复上述步骤，直到商为0为止。

4. 将所有得到的余数按照从最后一步到第一步的顺序排列，就得到了二进制数。

举个例子，将十进制数23转换成二进制数的步骤如下：

1. 23 ÷ 2 = 11 余 1

2. 11 ÷ 2 = 5 余 1

3. 5 ÷ 2 = 2 余 1

4. 2 ÷ 2 = 1 余 0

5. 1 ÷ 2 = 0 余 1

按照从最后一步到第一步的顺序，将余数排列起来，得到二进制数“10111”。

所以，十进制数23转换成二进制数是“10111”。

三、转换中的注意事项

在二进制转十进制的过程中，需要特别注意每一位的权值计算，确保每一位上的数字都乘以了正确的权值。而在十进制转二进制的过程中，则需要耐心地进行除法运算，确保每一步的商和余数都计算正确，并按照正确的顺序排列余数。

另外，二进制数在计算机中通常以补码的形式存储。补码是一种表示负数的方法，它的计算方法是先将数的绝对值转换为二进制，然后取反（即将每一位上的0变为1，1变为0），最后加1。在将二进制数转换为十进制数时，如果二进制数是补码形式，需要先将其转换为原码（即负数），然后再进行计算。

四、应用场景

二进制与十进制之间的转换在计算机科学和数字电路中有着广泛的应用。例如，在计算机编程中，经常需要将整数转换为二进制数来进行位运算；在数字电路设计中，二进制数被用来表示开关状态（开为1，关为0），从而实现对电路的控制。

此外，在数据传输和存储中，二进制数也发挥着重要作用。由于二进制数只有0和1两个状态，因此非常适合用于数字信号的传输和存储。在计算机网络中，数据通常以二进制形式进行传输，这样可以确保数据的准确性和可靠性。而在数据存储方面，二进制数也被广泛应用于磁盘、内存等存储设备中。

五、实践练习

为了更好地掌握二进制与十进制之间的转换方法，可以进行一些实践练习。例如，选择一些十进制数进行转换练习，将它们转换为二进制数并验证结果的正确性；同时，也可以选择一些二进制数进行转换练习，将它们转换为十进制数并验证结果的正确性。通过不断地练习和实践，可以逐渐提高对二进制与十进制之间转换的熟练度和准确性。

结语

二进制与十进制之间的转换是计算机科学和数字电路中的基础知识之一。掌握了这个知识点后，可以更加深入地理解计算机的工作原理和数字电路的设计方法。希望本文能够帮助读者更好地理解二进制与十进制之间的转换方法，并在实践中加以应用。通过不断地学习和实践，相信读者一定能够掌握这个重要的知识点并运用到实际工作中去。