十进制如何转换为二进制
在计算机科学和信息处理领域,理解十进制与二进制之间的转换至关重要。十进制是我们日常生活中最常用的数制,而二进制则是计算机内部数据处理的基础。掌握十进制转换为二进制的方法,可以帮助我们更好地理解计算机的工作原理,以及进行编程和数据分析等任务。下面,我们就来详细探讨一下十进制如何转换为二进制。
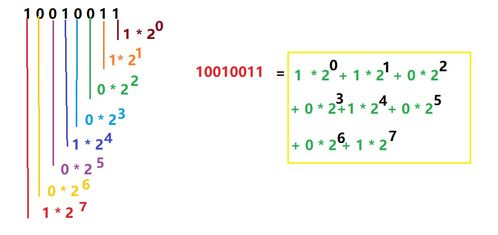
一、理解十进制与二进制的基本概念
十进制,即我们通常所说的“自然数”数制,是以10为基数的数制。它包含了0到9这十个数字,每一位上的数字乘以对应的权值(10的幂次方),然后求和,即可得到该十进制数的值。
二进制,则是以2为基数的数制。它只包含0和1这两个数字,每一位上的数字乘以对应的权值(2的幂次方),然后求和,即可得到该二进制数的值。由于计算机内部电路的逻辑状态只有开和关两种,因此二进制非常适合用于计算机的数据表示。
二、十进制转换为二进制的方法
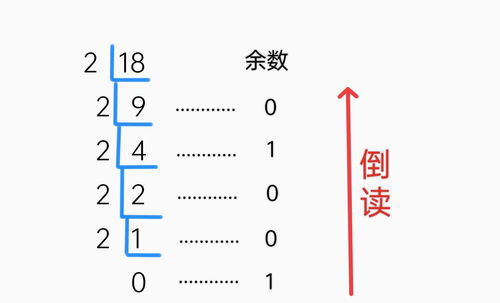
1. 除2取余法
除2取余法是一种直观且易于理解的十进制转二进制的方法。具体步骤如下:
(1)将十进制数除以2,得到商和余数(1或0)。
(2)将商再次除以2,重复上述步骤,直到商为0为止。
(3)将每一步得到的余数从低位到高位依次排列,即可得到该十进制数的二进制表示。
例如,将十进制数23转换为二进制:
23 ÷ 2 = 11 余 1
11 ÷ 2 = 5 余 1
5 ÷ 2 = 2 余 1
2 ÷ 2 = 1 余 0
1 ÷ 2 = 0 余 1
将余数从低位到高位排列,得到23的二进制表示为10111。
2. 乘2取整法
乘2取整法也是一种十进制转二进制的方法,但相对于除2取余法来说,它不如后者直观。具体步骤如下:
(1)将十进制数的小数点左移一位(相当于乘以2),并记录下整数部分是否为1。
(2)如果整数部分为1,则在当前二进制数的最高位上记1;如果整数部分为0,则记0。
(3)将小数部分重复上述步骤,直到小数部分为0或达到所需的精度为止。
(4)将每一步得到的二进制数从高位到低位依次排列,即可得到该十进制数的二进制表示(对于整数部分,最高位之前可能需要补0以保持位数的一致性)。
需要注意的是,乘2取整法主要用于处理十进制小数部分转换为二进制的情况。对于整数部分,仍然建议使用除2取余法。
三、十进制转换为二进制的实例分析
为了更好地理解十进制转换为二进制的过程,我们来看几个具体的实例:
1. 将十进制数42转换为二进制:
42 ÷ 2 = 21 余 0
21 ÷ 2 = 10 余 1
10 ÷ 2 = 5 余 0
5 ÷ 2 = 2 余 1
2 ÷ 2 = 1 余 0
1 ÷ 2 = 0 余 1
将余数从低位到高位排列,得到42的二进制表示为101010。
2. 将十进制数0.625转换为二进制(使用乘2取整法):
0.625 × 2 = 1.25,整数部分为1,记1
0.25 × 2 = 0.5,整数部分为0,记0
0.5 × 2 = 1,整数部分为1,记1
由于小数部分已经为0,所以转换结束。将得到的二进制数从高位到低位排列(并补上一个隐含的0表示整数部分为0),得到0.625的二进制表示为0.101。
四、十进制转换为二进制的注意事项
1. 在进行十进制转换为二进制时,要确保理解每一步的运算过程,以便能够准确地得到结果。
2. 对于整数部分和小数部分,可以根据需要选择不同的转换方法(如除2取余法或乘2取整法)。但在实际应用中,除2取余法更为常用且易于理解。
3. 在处理小数部分转换为二进制时,由于精度限制和二进制表示的特性(无法精确表示所有十进制小数),可能需要进行适当的取舍或截断。
4. 在进行大规模数据处理或编程时,可以使用编程语言中的内置函数或库来自动完成十进制与二进制之间的转换工作,以提高效率和准确性。
五、总结
十进制转换为二进制是计算机科学和信息处理领域中的基础知识之一。通过理解十进制与二进制的基本概念以及掌握具体的转换方法(如除2取余法和


























相关文章