在探讨随机事件和不确定性时,概率无疑是一个核心概念。概率计算不仅在数学、统计学、物理学、经济学等多个学科中占据重要地位,还在日常生活决策中发挥着关键作用。本文将从概率的基本定义出发,详细探讨几种常见的概率计算公式,并通过实例说明如何应用这些公式。
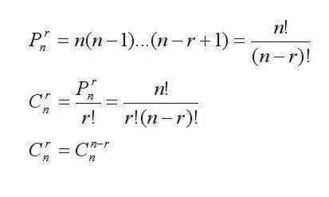
概率的基本定义
概率是对随机事件发生的可能性的度量,通常用P表示。一个随机事件E的概率P(E)的值介于0和1之间,即0 ≤ P(E) ≤ 1。其中,P(E) = 0表示事件E不可能发生,P(E) = 1表示事件E是必然事件。
古典概型与计算
古典概型是最基本、最简单的概率模型,它假设样本空间中的样本点(即基本事件)是有限的,且每个基本事件发生的可能性相同。
古典概型的计算公式
对于古典概型,事件E的概率P(E)等于事件E包含的基本事件数除以样本空间中的基本事件总数,即
P(E) = 事件E包含的基本事件数 / 样本空间中的基本事件总数
例如,抛掷一枚公平的六面骰子,每个面朝上的概率是1/6,因为样本空间(即所有可能的结果)包含6个基本事件(每个面朝上一次),而事件“3点朝上”只包含一个基本事件。
条件概率与乘法公式
条件概率是指在某个条件下,某事件发生的概率。条件概率的计算公式为:
P(A|B) = P(AB) / P(B),其中P(B) ≠ 0
这里,P(AB)表示事件A和事件B同时发生的概率,P(B)是事件B发生的概率,P(A|B)表示在事件B发生的条件下,事件A发生的概率。
乘法公式
利用条件概率,可以得到乘法公式:
P(AB) = P(A|B)P(B) = P(B|A)P(A)
这个公式表明,两个事件同时发生的概率等于其中一个事件在另一个事件发生的条件下的概率与另一个事件发生的概率的乘积。
全概率公式与贝叶斯公式
全概率公式和贝叶斯公式是解决复杂概率问题的有力工具。
全概率公式
如果事件B1, B2, ..., Bn构成一个完备事件组,即它们两两互斥,且它们的并集是样本空间S,那么对于任一事件A,有
P(A) = Σ P(A|Bi)P(Bi),i = 1, 2, ..., n
这个公式将事件A的概率表示为A在每个完备事件Bi发生的条件下的概率与Bi的概率的乘积之和。
贝叶斯公式
贝叶斯公式是全概率公式的逆应用,用于在已知事件A发生的条件下,求导致A发生的某个原因Bi的概率。公式为:
P(Bi|A) = P(A|Bi)P(Bi) / Σ P(A|Bj)P(Bj),j = 1, 2, ..., n
这个公式在统计推断、机器学习等领域有广泛应用。
独立事件与概率加法公式
独立事件
如果事件A的发生不影响事件B的发生概率,即P(AB) = P(A)P(B),则称事件A与事件B是相互独立的。
概率加法公式
对于任意两个事件A和B,有
P(A∪B) = P(A) + P(B) - P(AB)
如果A和B是互斥事件(即A和B不能同时发生),则P(AB) = 0,此时公式简化为
P(A∪B) = P(A) + P(B)
几何概率与连续概率分布
几何概率
几何概率涉及在几何空间中随机选择点或区域,计算某个特定区域被选中的概率。几何概率的计算通常涉及面积、体积等几何量的比值。
连续概率分布
对于连续随机变量,其概率不再用点概率表示,而是用概率密度函数描述。连续随机变量在某个区间内的概率等于该区间上概率密度函数的积分。
例如,正态分布是连续概率分布的一种,其概率密度函数为钟形曲线,用于描述许多自然现象和实验数据的分布。
应用实例
决策分析
在决策分析中,概率计算用于评估不同决策方案的风险和收益。例如,在投资决策中,可以通过计算不同市场情景下的收益概率,来选择最优投资组合。
质量控制
在质量控制中,概率计算用于评估产品的合格率、缺陷率






























相关文章