直角三角形的面积公式是几何学中的一个基础且重要的概念,它帮助我们快速计算直角三角形所围成的区域大小。在解决与直角三角形相关的实际问题时,这一公式显得尤为重要。下面,我们就来详细探讨一下直角三角形的面积公式及其应用。
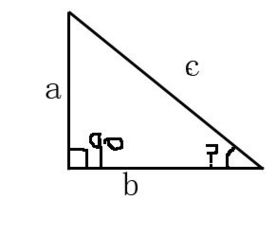
直角三角形是一种具有一个90度内角的三角形。由于其特殊的性质,直角三角形的面积计算变得相对简单。直角三角形的面积公式为:面积 = (底 × 高)/ 2。这里的底和高是构成直角三角形直角边的两条边。需要注意的是,在计算时,我们可以选择直角三角形的任意一条直角边作为底,另一条直角边则作为高。无论选择哪两条边作为底和高,计算出来的面积结果都是一样的。
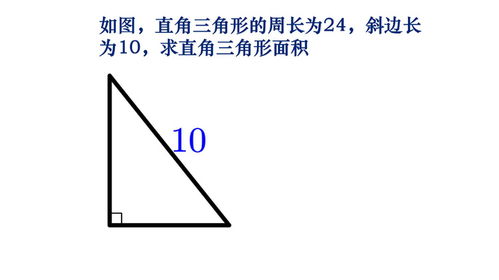
为了更好地理解这个公式,我们可以通过一个具体的例子来进行说明。假设我们有一个直角三角形,其中一条直角边的长度为3厘米,另一条直角边的长度为4厘米。根据直角三角形的面积公式,我们可以计算出这个三角形的面积为:(3厘米 × 4厘米)/ 2 = 6平方厘米。
直角三角形的面积公式不仅适用于简单的直角三角形,还可以扩展到更复杂的几何图形中。例如,在计算不规则多边形的面积时,我们可以将其划分为若干个直角三角形,然后分别计算每个三角形的面积,最后将它们相加得到整个多边形的面积。这种方法被称为“分割法”,是计算复杂图形面积的一种常用手段。
此外,直角三角形的面积公式在解决一些实际问题时也具有重要的应用价值。例如,在建筑设计中,我们可能需要计算一个直角三角形墙面的面积,以便确定所需的涂料数量。在农业生产中,我们也可能需要计算一个直角三角形田地的面积,以便合理安排种植计划。这些实际问题都可以通过应用直角三角形的面积公式来得到准确的答案。
除了面积公式外,直角三角形还有一些其他的重要性质,这些性质在解决几何问题时同样具有重要意义。例如,勾股定理是直角三角形的一个重要性质,它告诉我们直角三角形的两条直角边的平方和等于斜边的平方。这个定理在解决直角三角形相关的计算问题时非常有用。
此外,直角三角形的斜边也是其重要的特征之一。斜边是直角三角形中最长的一条边,它位于直角的对面。在解决直角三角形相关的问题时,我们有时需要利用斜边的长度来计算其他未知量。例如,在已知直角三角形的两条直角边长度的情况下,我们可以利用勾股定理来计算斜边的长度。反过来,如果我们已知斜边的长度和其中一条直角边的长度,我们也可以利用勾股定理来求解另一条直角边的长度。
在解决直角三角形相关的问题时,我们还需要注意一些常见的误区。例如,有些人在计算直角三角形的面积时,可能会误将斜边作为底或高来计算,这是不正确的。因为斜边并不是构成直角边的两条边之一,所以不能用斜边来计算直角三角形的面积。另外,有些人在利用勾股定理计算直角三角形的边长时,也可能会忽略单位的一致性,导致计算结果出现错误。因此,在解决直角三角形相关的问题时,我们需要认真审题,明确题目要求,并严格按照公式和定理进行计算。
此外,直角三角形还有一些特殊的情况,如等腰直角三角形和30-60-90直角三角形等。这些特殊情况下的直角三角形具有一些特殊的性质,可以帮助我们更快地解决问题。例如,在等腰直角三角形中,两条直角边的长度是相等的,这使得计算变得更加简单。在30-60-90直角三角形中,我们可以利用已知的边长比例关系来求解未知量,从而提高计算效率。
总的来说,直角三角形的面积公式是几何学中的一个基础且重要的概念。它不仅可以帮助我们快速计算直角三角形的面积,还可以扩展到更复杂的几何图形中,帮助我们解决各种实际问题。同时,直角三角形的其他重要性质也为解决相关问题提供了有力的工具。因此,在学习几何学时,我们需要深入理解并掌握直角三角形的相关知识,以便更好地应用它们来解决实际问题。
通过对直角三角形的面积公式的探讨,我们可以发现数学中的许多概念都是相互关联、相互支持的。一个看似简单的公式背后,往往隐藏着丰富的数学知识和应用价值。因此,在学习数学时,我们需要注重培养自己的逻辑思维能力和问题解决能力,善于从多个角度思考和解决问题。只有这样,我们才能更好地掌握数学知识,并将其应用于实际生活中。
































相关文章