直角三角形是几何学中的一个基础而重要的概念,它在各种实际应用中广泛出现,如建筑设计、工程测量、物理计算等。掌握直角三角形的基本性质和计算方法,对于理解和解决实际问题至关重要。其中,直角三角形的面积计算是基本且实用的知识点之一。本文将详细介绍直角三角形的面积计算公式,并探讨其应用与推导过程。
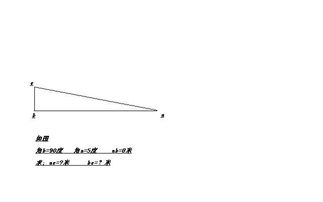
直角三角形是一种特殊的三角形,其中一个角为90度,其余两个角之和也为90度。根据直角三角形的定义,其边长关系可以用勾股定理来表示,即直角边的平方和等于斜边的平方(a² + b² = c²)。在直角三角形的面积计算中,我们主要关注直角边,因为直角三角形的面积与其两个直角边直接相关。
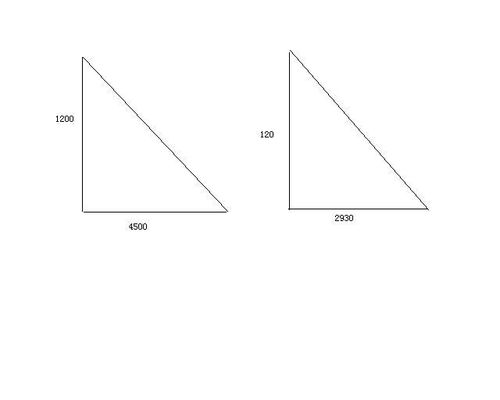
直角三角形面积的计算公式为:面积 = (直角边1 × 直角边2) ÷ 2。这里的直角边1和直角边2是直角三角形的两条直角边,即与直角相邻的两条边。公式中的“÷ 2”来源于三角形面积计算的一般公式(底 × 高 ÷ 2),在直角三角形中,可以将任意一条直角边视为底,另一条直角边视为高,从而应用这一公式。
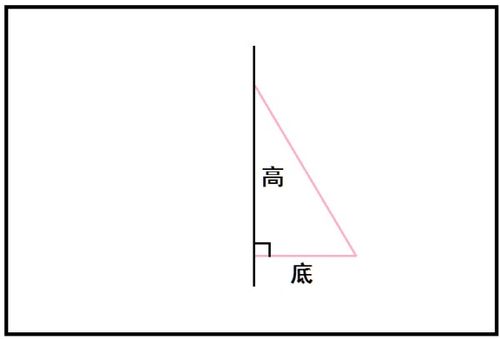
为了更直观地理解这个公式,我们可以通过一个实例进行说明。假设我们有一个直角三角形,其中一条直角边的长度为3厘米,另一条直角边的长度为4厘米。根据直角三角形面积的计算公式,其面积可以计算为:面积 = (3厘米 × 4厘米) ÷ 2 = 6平方厘米。这样,我们就可以快速而准确地计算出直角三角形的面积。
直角三角形面积的计算公式不仅简单实用,而且具有广泛的应用价值。在日常生活和工作中,我们经常需要计算直角三角形的面积,以解决各种实际问题。例如,在建筑设计中,我们可能需要计算一个直角三角形墙面的面积,以确定所需的涂料数量;在工程测量中,我们可能需要计算一个直角三角形地块的面积,以进行土地规划和利用;在物理计算中,我们可能需要计算一个直角三角形形状的物体的面积,以计算其受力情况或散热面积等。
此外,直角三角形面积的计算公式还可以与其他几何知识相结合,解决更复杂的几何问题。例如,在解决与直角三角形相关的几何问题时,我们可以利用面积公式来验证勾股定理的正确性,或者利用面积公式来求解直角三角形中的未知边长或角度等。
在探讨直角三角形面积的计算公式时,我们还需要注意其推导过程。虽然这个公式看起来很简单,但其背后蕴含着深刻的几何原理。直角三角形面积的计算公式可以从三角形面积的一般公式推导而来。在三角形中,我们可以将任意一条边视为底,从这条边到三角形顶点的垂线视为高,从而计算出三角形的面积。在直角三角形中,我们可以将任意一条直角边视为底,另一条直角边视为高,直接应用三角形面积的一般公式进行计算。这种推导过程不仅有助于我们理解直角三角形面积的计算公式,还可以帮助我们更好地掌握三角形面积的一般计算方法。
此外,直角三角形面积的计算公式还可以与其他数学知识相结合,进行更深入的研究和应用。例如,在解析几何中,我们可以利用直角三角形的面积公式来计算平面上两个向量之间的夹角;在三角函数中,我们可以利用直角三角形的面积公式来推导正弦、余弦等三角函数的性质和应用等。
在实际应用中,我们还需要注意直角三角形的面积公式与其他相关公式的区别和联系。例如,在直角三角形中,我们还可以利用斜边和其中一个锐角来计算面积,但这需要使用到三角函数的知识,并且计算过程相对复杂一些。相比之下,利用直角边计算面积的方法更加直观和简单,因此在大多数情况下更为常用。
总之,直角三角形的面积计算公式是几何学中的一个基本而重要的知识点。它简单实用,具有广泛的应用价值,可以帮助我们解决各种实际问题。同时,它还可以与其他几何知识和数学知识相结合,进行更深入的研究和应用。因此,我们应该熟练掌握直角三角形面积的计算方法,并在实际应用中灵活运用这一公式来解决问题。
通过本文的介绍,我们可以清晰地看到直角三角形面积计算公式的重要性和应用价值。无论是在学习几何知识的过程中,还是在解决实际问题时,我们都需要充分利用这一公式来进行计算和验证。同时,我们也应该不断学习和探索更多的几何知识和数学知识,以丰富我们的知识体系和解决问题的能力。希望本文的介绍能够帮助读者更好地理解直角三角形面积的计算公式,并在实际应用中取得更好的效果。
































相关文章